本スパン表では部材を単純梁とし、曲げモーメント、せん断力、たわみを求めるのに以下の計算式を用います。

a) 等分布荷重

図 22のように部材に等分布荷重のみがかかる場合、各計算式は以下のようになります。

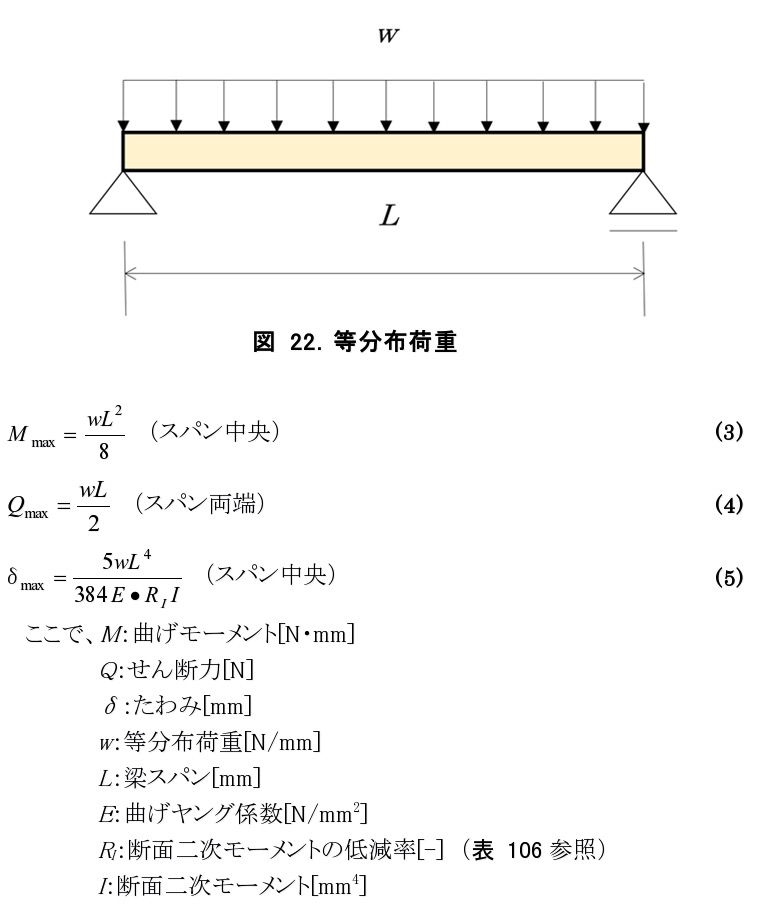
b) 集中荷重

図 23ように部材に集中荷重のみがかかる場合、各計算式は以下のようになります。

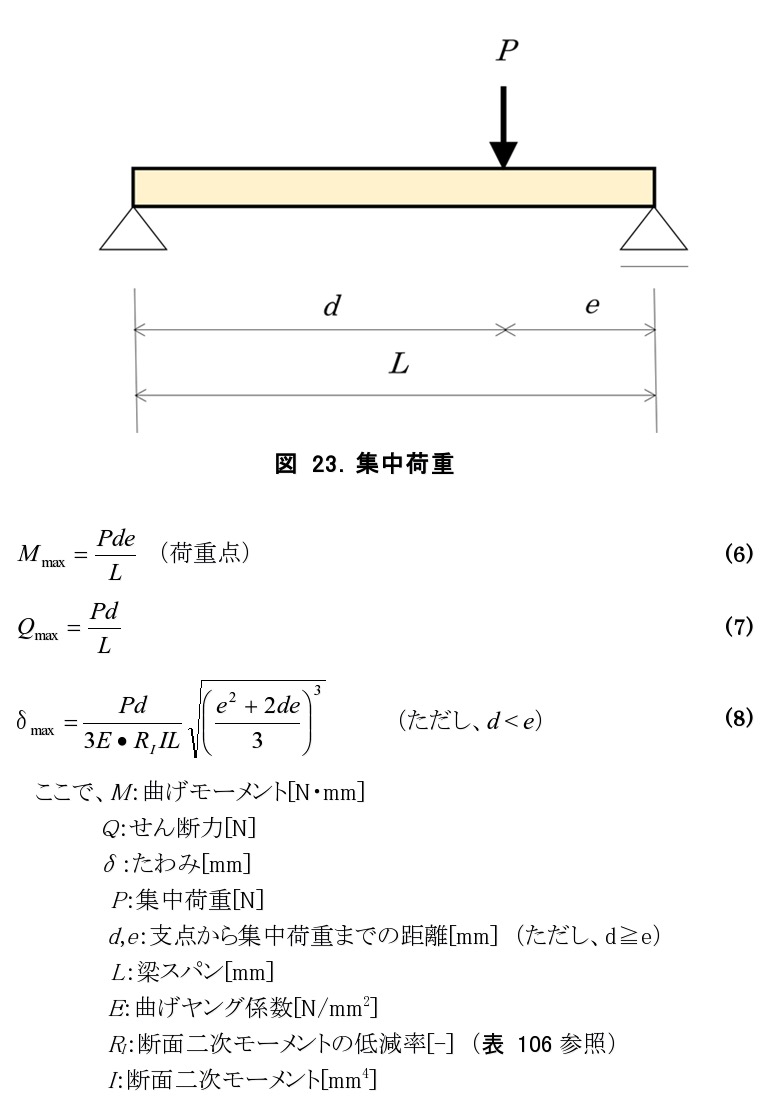
c) 荷重の組合せ

等分布荷重と集中荷重が存在する場合、それぞれの荷重により生じる曲げモーメント、せん断力、たわみを加算します。
複数の集中荷重が存在する場合、曲げモーメント、せん断力、たわみは以下のように扱います。

ⅰ)集中荷重が2点の場合

＜曲げモーメント＞
複数の集中荷重が存在する場合、最大曲げモーメントを単純に加算すると曲げモーメントを過大に評価してしまうことになります。従いまして、まず図 24のように、P1荷重点における曲げモーメントの合成M1合成と、P2荷重点における曲げモーメントの合成M2合成を考えます。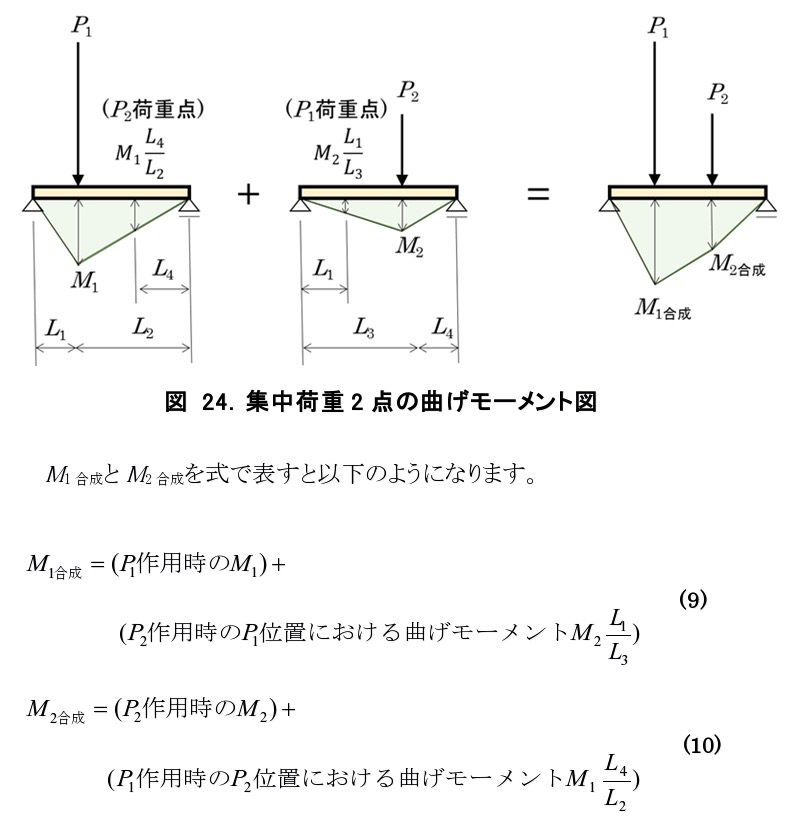 M1合成とM2合成を比較し、大きい方を集中荷重P1、P2による最大曲げモーメントとします。

＜せん断力＞
左右非対称に集中荷重がかかると、右から計算したせん断力と左から計算したせん断力が異なることがあるので、左右比較して最大せん断力を求めます。まず図 25のように集中荷重が2点かかる場合、P1によるL1間のせん断力Q1左、P1によるL2間のせん断力Q1右、P2によるL3間のせん断力Q2左、P2によるL4間のせん断力Q2右を以下のように計算します。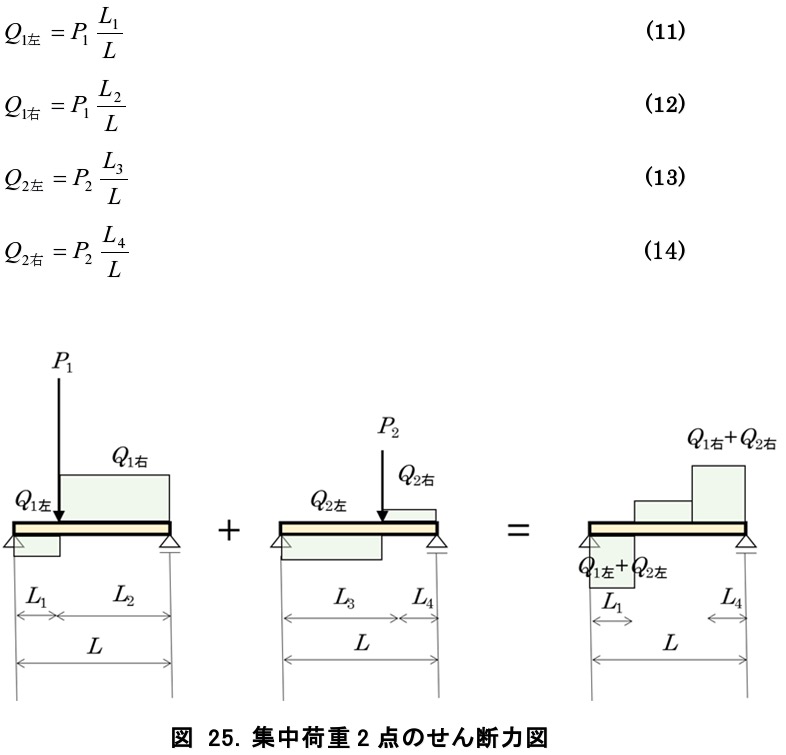 そして、左から計算したせん断力Q1左+Q2左と、Q1右+Q2右を比較し、大きい方を集中荷重P1、P2による最大せん断力とします。

＜たわみ＞
集中荷重P1による最大たわみδ1と集中荷重δ2による最大たわみを加算します。（δ1+δ2）

ⅱ)集中荷重が3点以上の場合

集中荷重が3点以上の場合、図 26のように集中荷重を等分布荷重と見なして、曲げモーメント、せん断力、たわみを計算します。 図 26のとき、見なし等分布荷重wは以下のようになります。